Introduccion a la Investigacion Operativa
1.- Introducción
Cuando una persona se enfrenta por vez primera con el término Investigación de Operaciones, no suele ser conocedora de las características específicas de esta ciencia ni de su objeto de estudio.
Además, la Investigación Operativa puede tener componentes muy diversos dependiendo de su área de aplicación concreta: Administración de Empresas, Ingeniería u otras. El objeto de estudio de la Investigación Operativa es la toma científica de decisiones mediante el empleo de técnicas cuantitativas. Es importante tener esta definición clara y, de esta forma, nos daremos cuenta de la amplitud de campo de la Investigación Operativa (IO).
Con demasiada frecuencia se ha hecho demasiado hincapié en los modelos de Programación Lineal dentro de la Investigación Operativa, lo cual ha dificultado la distinción entre ambos términos. Lo cierto es que la Programación Lineal es sólo una parte de la Investigación Operativa aunque, sin duda, una de las más importantes. Otras áreas o secciones habituales en el estudio de la Investigación Operativa son las siguientes (esta relación no es exhaustiva, sino que sólo pretende dar una idea de la extensión de la Investigación Operativa):
a) Programación entera
b) Problemas de transporte
c) Análisis de grafos y de redes. PERT y CPM.
d) Programación dinámica
e) Teoría de juegos.
f) Programación no lineal.
g) Teoría de colas.
h) Teoría de inventarios
i) Procesos markovianos de decisión. Análisis de decisión.
j) Simulación
k) Fiabilidad
Existen, de este modo, otras áreas –además de la Programación Lineal- en las que la Investigación Operativa
ejerce también su estudio. Es claro pues que la Investigación Operativa es una ciencia multidisciplinar que aparece en muchos campos del ámbito industrial, empresarial y de la administración pública. De hecho, con la aparición de la Programación Lineal en los años 40, aparece el sentimiento de dar una cohesión o visión de conjunto a todas las técnicas anteriormente enunciadas. Esa visión cohesionada, junto con el concepto de sistema, permite la aparición de la Investigación de Operaciones como ciencia.
Las subdivisiones en las que se establece la Investigación Operativa tienen los siguientes elementos en común:
Son necesarios amplios conocimientos de matemáticas, es decir, del manejo de muchas técnicas matemáticas, aunque con inmediata aplicación a la realidad.
Es necesario que, al final de cada problema definido, haya una decisión que tomar.
Es preciso definir un modelo que dé cauce a la toma de decisiones.
En el estudio de la Investigación Operativa se puede hacer más énfasis en los aspectos teóricos de los modelos matemáticos o bien en los aspectos prácticos. Estudiar de forma exclusiva modelos matemáticos, aun siendo importante para la Investigación Operativa, no constituye el principal ejercicio de la Investigación Operativa: es necesario verificar la aplicabilidad de los resultados que se deriven de los modelos matemáticos.
También a nivel introductorio se pueden visitar algunas de las siguientes páginas web:
http://www.informs.org/ Sociedad Americana de Investigación Operativa.
http://www.ifors.org/ Federación Internacional de Sociedades de Investigación de Operaciones.
http://www.orie.cornell.edu/ Departamento de Investigación Operativa de la Universidad de Cornell en Nueva York.
http://www.worms.ms.unimelb.edu.au/ Información genérica sobre Investigación Operativa.
En este sentido, hay que destacar que las técnicas de Investigación Operativa tienen un auge inusitado en los Estados Unidos. Algunos de los motivos de este auge son:
a) razones históricas,
b) la cultura empresarial americana, y
c) la dimensión del mercado americano. En Europa, cada vez se aplican más estas técnicas pero, con frecuencia, con un acento mucho más teórico. Entre los países europeos que más aplican las técnicas de la Investigación Operativa se pueden destacar los siguientes:
Gran Bretaña, Holanda, Francia y Alemania. Con el fenómeno de la globalización económica, cada vez son más las empresas multinacionales que emplean técnicas de Investigación Operativa para la toma científica de decisiones.
Referencia Histórica de la Investigación Operativa
Suele ser difícil hacer una referencia histórica de la Investigación Operativa. Principalmente,
porque no es sencillo establecer sus orígenes. Como se ha comentado anteriormente, muchas son las áreas que componen la Investigación Operativa, y hasta que apareció un elemento aglutinador en los años 40 del siglo XX, cada área tuvo su propia referencia histórica, haciendo muy difícil establecer la fecha exacta del nacimiento de la Investigación Operativa. No obstante, procuraremos dar unas pinceladas al respecto.
La necesidad de tomar decisiones es tan antigua como el hombre mismo, por ello, hemos de preguntarnos por qué la Investigación Operativa nace en un momento histórico preciso. Esto fue así, porque la realidad humana se fue complicando poco a poco y las decisiones que en un principio eran triviales, se convirtieron en decisiones difíciles. Con la llegada de la Revolución Industrial, la sociedad se hizo mucho más compleja y las decisiones habían de tomarse con más cuidado porque involucraban a más personas en sus consecuencias. Veamos a continuación lo que esto supuso históricamente.
Proceso Introductorio
Las diferentes ciencias han de ser comprendidas con profundidad antes de poder ser analizadas desde un punto de vista histórico. Quizás no sea fácil establecer los orígenes de la Investigación Operativa, porque no se tuvo conciencia de la misma hasta mucho más tarde de que algunas de sus ramas nacieran y se desarrollaran. No obstante, es necesario relacionar el alumbramiento de la Investigación de Operaciones, por lo menos nominalmente, con el transcurso de la II Guerra Mundial. Por esta razón, hemos de pensar en los orígenes de la ciencia operacional como en los de una técnica de naturaleza militar.
Dichos orígenes han supuesto una impronta decisiva en el tratamiento de las técnicas operacionales. En este sentido, cuando se pretende trazar una historiografía de una ciencia es muy importante delimitar la frontera de la misma en los terrenos conceptual e histórico.
Prolegómenos y rudimentos de la Investigación Operativa: la ciencia de la gestión
Después del proceso introductorio llegamos al momento delicado de establecer diferencias entre la Investigación de Operaciones y la Ciencia de la Gestión (o de la Administración). Entendemos por Ciencia de la Gestión (traducción del término inglés Management Science) la aplicación de los métodos y técnicas de la ciencia actual a los problemas de toma de decisiones en la administración. Realmente, esta misma definición podría valer también para Investigación Operativa, aunque ésta necesite de un manejo más explícito de técnicas matemáticas. Por tanto, estas dos ciencias pueden darse en el momento presente como equivalentes o sinónimas. No obstante, se puede comprender que la gestión y la organización han sido necesarias para la humanidad desde sus albores.
La necesidad de planificación y organización aparece ya en el antiguo Egipto hacia el año 4.000 a.C. y se va desarrollando a través de toda la Antigüedad hasta el advenimiento del Imperio Romano. En Israel y China también aparecen tímidos escarceos de organización y dirección hacia el año 1.000 a.C. Nabucodonosor establece algunas ideas sobre control de la producción hacia el año 600 a.C. En Grecia, se desarrollan en el 350 a.C. los primeros métodos de organización del trabajo y del tiempo. Alrededor del año 30 a.C., Julio César establece diversas ideas de planificación, control y unidad de mando, que luego pone en práctica en todo el Imperio Romano.
Todos los estudios y planteamientos organizacionales de la Antigüedad tienen su proyección, que no su continuación, a lo largo de toda la Edad Media, en donde se aprovechan sin posteriores desarrollos. Durante el siglo XV, en la Italia renacentista se vuelven a plantear de nuevo las cuestiones organizativas y aparecen diversos estudios sobre costes y sobre control de existencias.
No es fácil establecer otros hitos acerca de la organización hasta el siglo XVIII, cuando Pierre de Montmort inicia sus primeras ideas directivas que luego dan lugar a la teoría de juegos.
Con los inicios de la I Revolución Industrial, el sentido y la forma de estudio de la Ciencia de la Gestión adquieren su ser más pleno. Por otra parte, el desarrollo de las matemáticas durante los siglos XVIII y XIX permite disponer de las herramientas necesarias para la futura construcción de la Investigación de Operaciones. De esta forma, en 1767, Gaspard Monge descubre la manera geométrica de resolver un programa lineal. Posteriormente, Adam Smith establece el principio de especialización en los trabajos, y Robert Owen, ya en el siglo XIX, realiza un estudio sobre tareas en un proceso productivo, y advierte de la necesidad de adiestramiento en las mismas por parte de los operarios. Una aportación fundamental la realiza Babbage, en 1832, construyendo lo que se podría llamar el primer computador digital, que vendría a ser el antecesor de los modernos ordenadores. A finales del siglo XIX, Joseph Wharton hace de la dirección estratégica e industrial un saber universitario. No obstante, el auge de las revoluciones industriales del XIX permiten establecer un caldo de cultivo adecuado para el estudio de la ciencia operacional. Así, Frederick W. Taylor y Henry L. Gantt, ante la necesidad de planificación de la producción, establecen el método científico de dirección y las gráficas de programación productiva (de Gantt), respectivamente. A partir de este momento aparece la aportación nuclear del siglo XX a la Investigación de Operaciones, sabiendo que es en esta centuria cuando se produce su nacimiento real.
Génesis de la Investigación Operativa en el siglo XX
Diversos hechos habían ocurrido en los albores de ese siglo, que luego ayudaron a la génesis de la ciencia operativa. Entre otros citaremos: a) los rudimentos de la teoría de colas, con A.K. Erlang, y b) la construcción del modelo económico del tamaño del lote, con F.W. Harris. Sin embargo, estos hitos que luego constituyeron elementos clave de la Investigación Operativa, no permitieron establecer la misma como un saber independiente.
Tiene sentido iniciar nuestra exposición en el momento en el que se tuvo una conciencia clara de que algo nuevo y diferenciador estaba naciendo en el ámbito de la teoría de la organización a gran escala. Este momento es el preludio de la II Guerra Mundial.
Podríamos decir que es hacia 1935 cuando Inglaterra se da cuenta de que necesita dar una respuesta adecuada al creciente poderío militar alemán. Por esta razón, el gobierno inglés urge a un grupo de científicos a que realicen experimentos que conduzcan a un mejor control del espacio aéreo. Fruto de esta experimentación aparece el radar, que constituye el inicio de la lucha por la supremacía aérea. Este grupo de investigadores tomó su base en Bawdsey, y por esta razón se llamó grupo de Bawdsey.
De forma paralela, otro grupo se estuvo estableciendo durante 1936 para desarrollar el experimento Biggin Hill, que permitía la simulación de aviones enemigos y su detección. La conjunción de estos dos grupos, permitió ofrecer a la RAF (Royal Air Force) una estructura operacional, para sus equipos materiales y humanos, que le posibilitó librar la batalla de Inglaterra en 1940-41. El grupo de Bawdsey fue dirigido en 1938 por A.P. Rowe, el cual acuñó la expresión 'Operations Research', que posteriormente se extendió dentro del ámbito científico al resto de países occidentales.
La batalla de Inglaterra se recrudece en el otoño de 1940. Por esta razón, se solicita la ayuda de P.M.S. Blackett, un físico que después conseguirá el Premio Nobel por sus trabajos en rayos cósmicos, con objeto de establecer una sección de Investigación Operativa dentro de los comandos de acción de la RAF. Del mismo modo, Blackett fue consultado en diciembre de 1941, sobre la posibilidad de constituir una sección similar dentro de la Armada. Dicha sección fue constituida en enero de 1942.
Cuando los Estados Unidos entran en la guerra, son conscientes de la necesidad de tales grupos operativos y de la constitución de secciones operacionales para el éxito de los mismos. De esta manera, constituyen en 1942 un grupo operacional de lucha antisubmarina (ASWORG - Anti-Submarine Warfare Operations Research Group) que recoge toda la experiencia inglesa desarrollada por Blackett. De forma similar, la Fuerza Aérea Americana estructura diversos grupos operacionales para llevar a cabo sus labores logísticas. Al final de la guerra, la Armada americana disponía de un departamento de Investigación Operativa compuesto por más de setenta científicos, y la Fuerza Aérea disponía de más de dos docenas de secciones operacionales.
No puede decirse que las potencias del Eje hicieran uso de las técnicas operacionales durante la II Guerra Mundial, mientras que el número de científicos e investigadores involucrados en Investigación Operativa en la contienda por parte de ingleses, americanos y canadienses superó los setecientos. Las aportaciones que hicieron todos estos investigadores supusieron un giro copernicano en la manera de concebir la Ciencia de la Gestión en los años siguientes. De alguna manera, todos estos estudiosos que trabajaban de manera aislada en los años treinta se aglutinaron holísticamente con ocasión de la guerra, y produjeron un conjunto de técnicas y teorías que ocasionaron el alumbramiento de la Investigación de Operaciones como ciencia.
El crecimiento de la Investigación Operativa, de 1945 a la actualidad
Es muy difícil condensar en unas líneas todo lo que han supuesto las décadas anteriormente mencionadas para la ciencia operacional, habida cuenta de su importancia y de la riqueza de trabajos producidos. Realmente, se ha construido más ciencia operacional durante estos
años que en todo el resto de la historia de la humanidad. Puede decirse, por tanto, que la verdadera historia de la Investigación Operativa se ha desarrollado durante este período: se han establecido líneas de investigación, han aparecido sociedades profesionales, se han creado revistas de investigación, se han publicado libros y se ha incluido la materia dentro del currículum educativo.
Una vez finalizó la contienda mundial y habida cuenta del éxito cosechado por las técnicas operativas, éstas continuaron desarrollándose dentro del ámbito militar, puesto que era el ejército quien poseía la mayor parte de los investigadores y quien estaba interesado en proseguir dicha línea de trabajo. A mediados de los años cincuenta se desplazó el centro de gravedad de interés de la Investigación Operativa, y alcanzó el terreno industrial y el académico. Aparece el interés por la Ciencia de la Gestión (Management Science). En la década de los setenta, ha continuado el desarrollo expansivo de la Investigación Operativa, llegando al ámbito de la administración pública, tratando los siguientes tipos de problemas: transporte urbano, administración de justicia, construcción de edificios públicos, educación, hospitales y servicios sociales. De esta manera, el peso investigador de la Investigación Operativa se desplaza desde el Reino Unido a los Estados Unidos, en donde se constituyen diversos institutos y organizaciones de estudio, como The Urban Institute (1968) y The New York City-Rand Institute (1969). También, son muchas las empresas que, a partir de los años cincuenta, se ayudan de técnicas operativas para diseñar sus políticas de producción y de distribución.
Por ejemplo, a partir de una encuesta que realiza Turban en 1972 en Estados Unidos sobre las 500 empresas más importantes del país (de acuerdo con la revista Fortune), se deduce que la mitad de las empresas que contestaron la encuesta poseían un departamento especial dedicado a tareas de Investigación de Operaciones o Ciencia de la Administración. No obstante, la Investigación Operativa forma cada día más, una parte de las actividades normales de la empresa moderna y, por tanto, ya no se trata de una función especializada que deba llevarse a cabo en un departamento separado. De acuerdo con este estudio las técnicas operacionales más empleadas eran el análisis estadístico, la simulación, la programación lineal, la teoría de inventarios y la programación dinámica. Otras técnicas empleadas, aunque de menor uso, eran la programación no lineal, las líneas de espera, la teoría de juegos, el análisis de decisión de Bayes y la programación entera.
Posteriormente, se realizaron otras encuestas de resultados similares: a) en 1977, Ledbetter y Cox (1977); b) en 1979, Thomas y DaCosta (1979); c) en 1983, Forgionne (1983). En todas ellas se comprueba cómo cada vez son mayores en número las técnicas operativas empleadas, y cómo dichas técnicas aparecen con más frecuencia en otras áreas o departamentos de la empresa. Estudios de otro tipo fueron los de Fabozzi y Valente (1976) que encuestaron, en 1976, mil compañías americanas en relación con el uso de la programación matemática (programación lineal, no lineal y dinámica). Estos autores descubrieron que era la dirección de Producción (mezclas de productos, asignación de recursos, diseño de planta y maquinaria,...) el área en donde más se aplicaba la Investigación de Operaciones dentro del ámbito de la empresa. En número de aplicaciones le seguía el área de Inversión y Financiación.
Especificaciones y concreciones históricas de la Investigación Operativa: la programación matemática
La Programación Matemática ha formado parte de la Investigación Operativa desde la constitución de la misma como ciencia hasta la actualidad. Sin embargo, muchos de los problemas tratados por la Programación Matemática eran conocidos desde mucho antes. Grandes matemáticos de los siglos XVIII y XIX, como Euler, Gauss y Lagrange trabajaron en problemas de optimización con restricciones y establecieron las primeras condiciones de optimalidad. Lo cual quiere decir que los problemas que la Programación Matemática planteaba en los años cuarenta de nuestro siglo no eran nuevos en su formulación, pero sí en su enfoque. Los métodos matemáticos clásicos no estaban pensados para una resolución en dimensiones altas, como iban a requerir las nuevas necesidades industriales. Esta fue la aportación de la ciencia operacional, máxime cuando se desarrollaron las técnicas computacionales que permitieron hacer realidad el cálculo rápido y a gran escala. La Investigación Operativa supuso un giro copernicano en la manera de tratar los programas matemáticos. Se implementaron algoritmos que computacionalmente eran más eficientes que los clásicos y, de esta manera, problemas que tradicionalmente habían sido complejos, ahora resultaron asequibles.
El cambio de mentalidad era notable y, por tanto, un nuevo modelo científico se estaba abriendo paso. Para el desarrollo de las distintas técnicas algorítmicas, era básico el estudio de los sistemas de desigualdad como habían hecho los matemáticos Julius Farkas, Jean Baptiste Fourier y T.S. Motzkin. El análisis de los problemas económicos se debe a John Von Neumann y a Abraham Wald. No obstante, cuando se trata de presentar una descripción histórica de la Programación Matemática, hay que tener en cuenta la gran aportación de Dantzig (foto de la derecha) con su método simplex para programación lineal. Este hito ha supuesto la demarcación de la época fundacional de la Programación Matemática. Dicho evento se ha considerado como el inicio de la Investigación Operativa, puesto que lo ha sido de la programación lineal, y ha traído consigo la resolución de muchos problemas operacionales.
Realmente, el nuevo estilo marcado por el método simplex ha construido el auténtico espíritu de la optimización matemática. No hay que olvidar la intención de Samuel Eilon al inventar el término satisfizar (fusión de satisfacer y optimizar) intentando describir la labor del investigador de operaciones: encontrar una solución satisfactoriamente (aceptablemente) óptima (o buena). De ahí procede la sentencia: "optimizar es la ciencia de lo esencial; satisfizar es el arte de lo factible" (Eilon (1972)).Realmente, en cuanto se intenta resolver un problema práctico surgido de la empresa o de la realidad económica se puede palpar la potencia del método simplex. A principios de la década de los sesenta, Abraham Charnes y William Cooper (1961) publicaron un libro de gran influencia para los años posteriores: Management Models and Industrial Applications of Linear Programming. Esta obra supuso un gran impacto en el desarrollo de la práctica y de las aplicaciones industriales de la programación lineal (principalmente en las compañías petrolíferas y químicas). Pudo comprobarse la potencia de esta nueva herramienta, a la hora de resolver los problemas decisionales de las grandes empresas. De igual modo, se aplicó la programación lineal a la teoría económica como muestran las aportaciones de Robert Dorfman, Paul Samuelson y Robert Solow (1958), o las de David Gale (1960), o bien las de Gérard Debreu (1963).
Nuevos desarrollos de la programación lineal
La Programación Lineal fue una de las primeras herramientas cuantitativas con la que contó la Investigación Operativa. Rápidamente se descubrió su eficiencia. Por esta razón, era muy interesante conseguir nuevos métodos de resolución que hicieran la competencia al algoritmo simplex.
Como una innovación destacable en los años ochenta aparece un nuevo y poderoso algoritmo para la resolución de programas lineales: en 1984, Narendra Karmarkar (1984) de AT&T Laboratories publicó un artículo presentando esquemáticamente un método para resolver programas lineales de gran tamaño. Este método llamado algoritmo de Karmarkar se presenta como un buscador de óptimos a partir de puntos interiores, siendo ésta la gran novedad en relación con el método simplex.
Dicho artículo de Karmarkar no describe totalmente el método resolutorio y, además, afirma que es mucho más rápido que el simplex para problemas de gran dimensión. El intento de descubrimiento de un remedo de dicho método puso a toda la comunidad científica en pie de búsqueda. Pasaron cuatro años hasta que se logró un conocimiento general del método y su distribución comercial. Esta extensión del algoritmo de Karmarkar fue debida a AT&T Laboratories, que llamó a esta versión 'AT&T KORBX Linear Programming System'. La instalación completa de esta versión tuvo un costo inicial de $8.900.000.
Desde un principio se realizaron multitud de comparaciones entre el método simplex y el de Karmarkar, con objeto de determinar cuál de los dos era el más eficiente. Sin embargo, esto no es fácil de determinar puesto que hay que especificar qué es exactamente lo que significa eficiencia. Es necesario efectuar la comparación en multitud de situaciones diversas y a partir de ellas establecer la correspondiente tesis. Se han realizado estudios que cotejan el método de Karmarkar con un paquete informático estándar del método simplex llamado MINOS. Para problemas de tamaño grande (a partir de varios miles de restricciones) las mejoras en tiempo de cálculo del método de Karmarkar sobre el simplex son notables (factores entre 10 y 50 son comunes). No obstante, esta situación no supone la supremacía del método de Karmarkar en todo tipo de problemas. No hay que olvidar que para problemas de dimensión pequeña, el método simplex es más intuitivo y fácil de aplicar.
También es posible realizar algunos comentarios acerca de la complejidad computacional de cada uno de los métodos. El método de Karmarkar es un algoritmo de tiempo polinomial, mientras que el simplex no goza de esta propiedad, sino que es de tiempo exponencial. De esta forma, tenemos explicada la razón por la cual el método de Karmarkar obtiene mejores resultados para problemas de gran dimensión.
Es llamativo que los problemas que hasta hace unos años necesitaban de computadoras de tamaño medio, ahora sean resolubles mediante ordenadores personales. En la actualidad, prácticamente cualquier usuario de la Investigación Operativa puede resolver problemas lineales mediante LINDO (u otro paquete informático semejante) en un ordenador portátil.
De esta manera, mediante LINDO se pueden manejar problemas con hasta 50.000 restricciones y 200.000 variables. De igual modo, se desarrolló el paquete MINOS (empleando para programación lineal el método simplex) en el Systems Optimization Laboratory del Departamento de Investigación Operativa de la Universidad de Stanford, que ha sido usado más frecuentemente como herramienta optimizadora en programación no lineal. Otros lenguajes de modelización se han desarrollado para ordenadores personales.
Así, ha aparecido GAMS/MINOS que es una combinación de los dos programas bien conocidos con objeto de construir un lenguaje de modelización algebraica implementado por IBM. De la misma forma, ha aparecido el paquete XPRESS-LP; y el lenguaje MPL (Mathematical Programming Language) desarrollado por Maximal Software en Islandia. Esta misma casa produjo la utilidad Turbo-Simplex.
En los años noventa fueron apareciendo otras utilidades informáticas, como son las hojas de cálculo y sus complementos asociados, capaces de resolver programas lineales. Entre algunos de estos complementos se pueden citar los siguientes: Solver, VINO, What's Best? y XA. Casi todas estas utilidades fueron construidas por IBM para sus propias computadoras, sin embargo, poco a poco, se van obteniendo versiones para Macintosh.
Aunque estas son las más recientes aplicaciones informáticas de los últimos cinco años, en los próximos años se mejorarán, a la vez que se extenderán los lenguajes y paquetes informáticos que permitirán resolver con relativa facilidad problemas de programación lineal complejos.
Introducción a la Programación Lineal.
En cualquier empresa, muchas de las decisiones que se toman tienen por objeto hacer el mejor uso posible (optimización) de los recursos de la misma. Por recursos de una empresa entendemos la maquinaria que ésta posea, sus trabajadores, capital financiero, instalaciones, y las materias primas de que disponga. Tales recursos pueden ser usados para fabricar productos (electrodomésticos, muebles, comida, ropa, etc.) o servicios (horarios de producción, planes de marketing y publicidad, decisiones financieras, etc.). La Programación Lineal (PL) es una técnica matemática diseñada para ayudar a los directivos en la planificación y toma de decisiones referentes a la asignación de los recursos.
Como ejemplos de problemas donde la Programación Lineal desarrolla un papel fundamental, podríamos citar:
A partir de los recursos disponibles, determinar las unidades a producir de cada bien de forma que se maximice el beneficio de la empresa.
Elegir materias primas en procesos de alimentación, para obtener mezclas con unas
determinadas propiedades al mínimo coste.Determinar el sistema de distribución que minimice el coste total de transporte, desde
diversos almacenes a varios puntos de distribución.Desarrollar un plan de producción que, satisfaciendo las demandas futuras de los productos de una empresa, minimice al mismo tiempo los costes totales de producción e inventario.
Características de un problema de Programación Lineal
Las técnicas de Programación Lineal han sido ampliamente utilizadas en ámbitos tan diferentes como el militar, industrial, financiero, de marketing, e incluso agrícola. A pesar de tal diversidad de aplicaciones, todos los problemas de Programación Lineal tienen cuatro propiedades comunes:
Pretenden optimizar (maximizar o minimizar) alguna cantidad (función objetivo). Así, por ejemplo, el principal objetivo de un banquero sería maximizar beneficios, mientras que el principal objetivo de una empresa transportista podría ser minimizar los costes de los envíos.
Habrá que tener en cuenta las restricciones que limitan el grado en el cual es posible modificar las variables que afectan a nuestra función objetivo. Así, a la hora de decidir cuántas unidades de cada bien se han de producir, deberemos considerar, entre otras, las limitaciones de personal y maquinaria de que disponemos.
El problema debe presentar distintas alternativas posibles: si una compañía produce cuatro bienes diferentes, la dirección puede usar Programación Lineal para determinar las cantidades de recursos que asigna a la producción de cada uno de ellos (podría optar por hacer una asignación ponderada, dedicar todos los recursos a la producción de un único bien abandonando la producción del resto, etc.).
En Programación Lineal, la función objetivo debe ser una función lineal, y las restricciones deben ser expresables como ecuaciones o inecuaciones lineales.
Planteamiento de un problema de Programación Lineal
Ejemplo: Una empresa fabrica dos modelos de mesas para ordenador, M1 y M2. Para su producción se necesita un trabajo manual de 20 minutos para el modelo M1 y de 30 minutos para el M2; y un trabajo de máquina de 20 minutos para M1 y de 10 minutos para M2. Se dispone de 100 horas al mes de trabajo manual y de 80 horas al mes de máquina. Sabiendo que el beneficio por unidad es de 1,5 y 1 € para M1 y M2, respectivamente, planificar la producción para obtener el máximo beneficio.
Nos limitaremos ahora a plantear formalmente el problema (ya lo resolveremos más adelante):
Llamando: X = “nº unidades producidas al mes de M1”, e Y = “nº unidades producidas al
mes de M2 ”, nuestra función objetivo sería: Maximizar:
Z(X,Y) = 1,5X + Y
y las restricciones vendrán dadas por:
Sujeto a:
20X + 30Y <= 100*60
20X + 10Y <= 80*60
X >= 0
Y >= 0
Las dos últimas restricciones, si bien no constan de forma explícita en el enunciado, sí figuran de forma implícita, pues el número de mesas a producir no puede ser inferior a 0.
Supuestos básicos de la Programación Lineal
Desde un punto de vista técnico, hay cinco supuestos que debe cumplir todo problema de programación lineal:
Los coeficientes, tanto de la función objetivo como de las restricciones, son conocidos con exactitud y además no varían durante el período de tiempo en que se realiza el estudio (supuesto de certidumbre).
Tanto en la función objetivo como en las restricciones hay proporcionalidad: si para la producción de un bien empleamos 5 horas de un determinado recurso (mano de obra, maquinaria, etc.), para producir diez unidades de dicho bien serán necesarias 50 horas del mismo recurso.
Aditividad de actividades: tanto en la función objetivo como en las restricciones, la contribución de cada variable es independiente de los valores del resto de las variables, siendo el total de todas las actividades igual a la suma de cada actividad individual. Así, por ejemplo, si producimos dos tipos de bienes, uno que nos reporte un beneficio de 20 €/unidad, y otro que nos reporte un beneficio de 10 €/unidad, la producción de un bien de cada tipo supondrá un beneficio total de 30 €.
Las soluciones del problema serán, en general, números reales no necesariamente enteros (supuesto de divisibilidad). Para aquellos problemas en los cuales sólo tenga sentido obtener soluciones enteras (cuando las soluciones se refieran a objetos indivisibles), se usarán técnicas de Programación Lineal Entera (PLE).
Las variables de nuestro modelo tomarán siempre valores positivos (supuesto de no negatividad), dado que no tiene sentido hablar de cantidades negativas de objetos físicos.
Resolución gráfica de un problema de Programación Lineal
El método gráfico de resolución tan sólo es aplicable a problemas con dos variables (X e Y). Para aquellos casos en que el número de variables del problema sea superior a dos, no será posible encontrar la solución a partir de un gráfico bidimensional y, por tanto, tendremos que usar métodos de resolución más complejos. Aún así, el método gráfico es de un gran valor pedagógico dado que nos permite vislumbrar de una forma intuitiva las ideas básicas de la Programación Lineal.
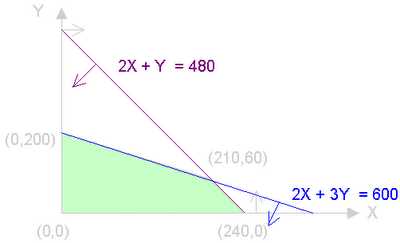
Volviendo al ejemplo de las mesas de ordenador, dado que en él tenemos sólo dos variables, podremos representar cada una de las restricciones en el plano real. Estas restricciones son semiespacios (por ser lineales), la intersección de los cuales se denomina región factible (área de color verde en la figura):
La teoría matemática establece que, dado un problema de Programación Lineal que tenga solución, ésta vendrá dada por uno de los vértices (o puntos extremos) del polígono que configura la región factible. Por tanto, será suficiente hallar las coordenadas de dichos vértices (intersecciones de rectas) y determinar (sustituyendo en la función objetivo) cuál de ellos es la solución óptima. En nuestro ejemplo, tendríamos sólo cuatro puntos candidatos a ser solución del problema (los cuatro vértices del polígono), sustituyendo sus coordenadas en la función objetivo obtenemos:
Z(0,0) = 0; Z(0,200) = 200; Z(210,60) = 375; y Z(240,0) = 360
Como en este caso buscábamos maximizar Z(X,Y), concluiremos que el punto óptimo es el (210,60), dado que con él obtenemos el valor máximo de la función objetivo. Así pues, la solución a nuestro dilema será fabricar 210 mesas de tipo M1 y sólo 60 de tipo M2, con ello conseguiremos unos beneficios de 375 €.
Casos especiales
A la hora de resolver un problema de Programación Lineal, nos podríamos encontrar con cualquiera de estas cuatro situaciones especiales que conviene conocer:
No Factibilidad: Podría ocurrir que el problema propuesto no tuviese solución. Éste sería el caso en que las restricciones fuesen incompatibles, i.e., que ningún punto del plano (o, en general, del espacio real n-dimensional) puede cumplir simultáneamente todas las limitaciones a las que estamos sometidos, es decir, la región factible es un conjunto vacío.
No Acotación: En ocasiones, podemos encontrarnos con problemas que no tengan una solución finita; así por ejemplo, en un problema de maximización podríamos tener alguna variable que pudiese incrementarse indefinidamente sin violar ninguna de las restricciones, permitiendo a la función objetivo tomar valores tan grandes como se desee. Gráficamente, tendríamos una región factible no acotada.
Redundancia: Algunas restricciones pueden “estar de más” por no aportar nada nuevo a la “forma” de la región factible, ya que hay otras que resultan ser más restrictivas (esto suele ocurrir en problemas extensos, donde resulta difícil reconocer restricciones redundantes).
Soluciones Múltiples: Un problema de Programación Lineal puede tener más de una solución óptima (e incluso infinitas). En el caso gráfico de dos variables, si dos vértices consecutivos de la región factible son solución óptima del problema, entonces todos los puntos del segmento comprendido entre ellos también serán óptimos.
Ejemplos de resolución gráfica
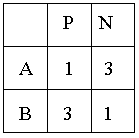
Ejemplo 1: La tabla adjunta muestra las unidades de nitrógeno (N) y de fósforo (P) que contiene cada kilo de los abonos A y B. Se desea obtener un abono que, como mínimo, contenga 9 unidades de N y 9 unidades de P. El precio de A es de 10 €/kg. y el de B es de 20 €/kg. Calcular las cantidades que deben comprarse de A y de B para satisfacer las necesidades minimizando el coste. Resolver el mismo ejercicio suponiendo que el precio de B es de 30 €/kg.
Llamando X = “nº kilos de A”, e Y = “nº kilos de B”,
Minimizar: Z(X,Y) = 10X + 20Y
Sujeto a: 3X + Y >= 9
X + 3Y >= 9
X , Y >= 0
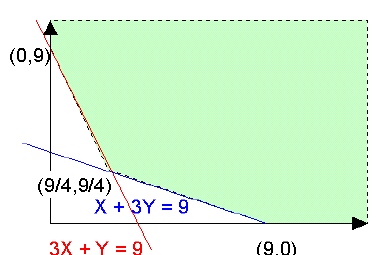
Evaluando Z(X,Y) en cada uno de los vértices:
Z(0,9) = 180; Z(9/4,9/4) = 67,5; Z(9,0) = 90
Por tanto, la solución óptima es utilizar 9/4 kilos de A y 9/4 kilos de B, lo que supone un coste (mínimo) de 67,5 € . Si ahora consideramos la nueva función objetivo
Z(X,Y) = 10X + 30Y, al evaluar en los vértices (las restricciones no han cambiado), obtenemos: Z(0,9) = 270; Z(9/4,9/4) = 90; Z(9,0) = 90 -> tendremos infinitas soluciones ya que cualquier punto del segmento que une los dos últimos vértices (éstos incluidos) será un óptimo, obteniéndose en ellos un coste (mínimo) de 90 €.
Ejemplo 2: Unos grandes almacenes desean liquidar 200 camisas y 100 pantalones de la temporada anterior. Para ello lanzan dos ofertas, A y B: la oferta A consiste en un lote de una camisa y un pantalón, que se vende a 30 €; y la oferta B consiste en un lote de tres camisas y un pantalón, que se vende a 50 €. No se desea ofrecer menos de 20 lotes de la oferta A ni menos de 10 de la B. ¿Cuántos lotes ha de vender de cada tipo para maximizar la ganancia?.
Sean:
X = “nº lotes tipo A”
Y = “nº lotes tipo B”
Maximizar: Z(X,Y) = 30X + 50Y
Sujeto a:
3X + Y <= 200 X + Y <= 100 X >= 20
Y >= 10
Evaluando en los vértices:
Z(20,80) = 4.600; Z(50,50) = 4.000; y Z(190/3,10) = 2.400
Observar que, en este caso, se hace innecesario calcular Z(20,10), pues es claro que su valor será inferior al de Z(20,80) y al de Z(190/3,10). En definitiva, pues, tendremos que la empresa debe vender 20 lotes de tipo A y 80 de tipo B, con lo que tendrá una ganancia (máxima) de 4.600 €.
Casos prácticos con software
Como ya hemos dicho, el método gráfico sólo permite resolver problemas con no más de dos variables. En caso de tener más de dos variables, necesitaremos utilizar métodos más complejos, como son el Algoritmo Simplex o el Algoritmo de Karmarkar. Estos algoritmos permiten, mediante una serie de pasos reiterativos (tablas), abordar problemas de Programación Lineal por muy complicados que éstos sean. En la práctica, sin embargo, resulta necesario utilizar algún programa de ordenador (como el LINDO o la macro Solver de Excel) el cual agilice los numerosos y repetitivos cálculos que exigen ambos algoritmos.
LINDO (Linear, Interactive, and Discrete Optimizer) es un programa sencillo de usar y muy potente que permite resolver extensos problemas de programación lineal, entera, e incluso cuadrática. Sus creadores (LINDO Systems, Inc.) permiten descargar de su página web (www.lindo.com) una versión de demostración gratuita que tolera hasta 150 restricciones y 300 variables (la versión profesional es capaz de trabajar con 50.000 restricciones y 200.000 variables).
Al iniciar LINDO (versión 6.1 para Windows), aparecen varias ventanas: la exterior (con la etiqueta “LINDO”) es la ventana principal, todas las demás ventanas que vayan apareciendo estarán contenidas dentro de ella. La ventana principal contiene también todos los menús de comandos y la barra de herramientas. Utilizaremos la ventana secundaria “
A continuación, se muestra cómo planteamos en LINDO el ejemplo anterior de las mesas de ordenador:
En este punto, es conveniente hacer notar las siguientes observaciones:
Podemos añadir comentarios personales sin más que anteponerles el signo de admiración!.
Siempre hemos de finalizar la formulación del problema añadiendo el comando END.
Por defecto, LINDO ya considera la no negatividad de las variables.
LINDO sólo acepta cinco operadores: + , - , <= , >= , e = . Así pues, en la formulación del problema no podrá usarse ningún otro operador ( * , / , ^ , etc.) ni tampoco paréntesis asociativos.
En la parte derecha de una desigualdad sólo se permiten valores numéricos, mientras que en la parte izquierda sólo se permiten expresiones lineales de variables y sus coeficientes.
El siguiente paso es pedirle a LINDO que resuelva el problema. Para ello es suficiente con hacer clic sobre el botón Solve (el que tiene forma de diana), o bien seleccionar esta opción en la barra de menús. LINDO intentará primero compilar el modelo formulado (para determinar si está bien planteado o no) y, en el caso de que la formulación sea incorrecta (ya sea desde un punto de vista matemático o de sintaxis), nos devolverá el siguiente mensaje:
An error ocurred during compilation on line: n
Si tras resolver un problema hacemos alguna modificación en la formulación del mismo, es necesario volver a compilar el modelo (Solve>Compile) antes de volver a usar Solve.
Si el modelo ha podido ser compilado, LINDO comenzará la resolución efectiva del problema, mostrando la ventana “Status”, donde se da información sobre el estado del proceso resolutivo:
A continuación se describen algunos de los campos que aparecen en la ventana anterior:
Status: ofrece el estado de la solución actual (óptima, factible, no factible, o no acotada).
Iterations: número de iteraciones (tablas del algoritmo) que se han realizado.
Infeasibility: cantidad por la cual las restricciones han sido excedidas o violadas.
Objective: valor actual de la función objetivo.
Elapsed time: tiempo transcurrido desde el inicio de la resolución.
Update Interval: la frecuencia (en segundos) en que esta ventana es renovada.
Cuando la resolución haya finalizado, el programa nos preguntará si queremos realizar un análisis de sensibilidad. De momento elegiremos la opción NO. Aparecerá una nueva ventana en la pantalla, la “Reports Window”, a la cual LINDO enviará todo el output en forma de texto:
Imagen 09
La información básica que nos proporciona esta ventana para nuestro ejemplo de las mesas es que se han necesitado dos iteraciones para llegar a dar con la solución óptima de fabricar 210 mesas del tipo M1 y 60 del tipo M2, con lo cual obtendremos un beneficio de 375 € (el máximo de los posibles bajo las restricciones que tenemos). Además, con este plan de producción estaremos agotando todos nuestros recursos, tanto el tiempo de mano de obra como el tiempo de máquina disponible (dado que la columna SLACK OR SURPLUS toma el valor 0 en ambas restricciones).
Como puede observarse el uso de LINDO es muy cómodo para el usuario de Programación Lineal. No necesita de conocimientos especializados, sino que tan sólo requiere del uso del sentido común. Está es la principal ventaja de esta herramienta en optimización lineal.
7.- Referencias Bibliográficas
Anderson, D.R., Sweeney, D. J. y Williams, T.A. (2001): Quantitative Methods for Business.West Publishing Company. (Existe versión en español)
Camm, J. y Evans, J.R. (2000):Management Science and Decision Technology. South Western College Publishing.
Faulin, J. (1998): “Introducción histórica al desarrollo e implantación de la Investigación Operativa”. Cuadernos de Bioestadística y sus aplicaciones informáticas. Vol.16, nº1, pp. 88-104.
Hillier, F.S. y Liebermann, G.J. (2001):Introducción a la Investigación de Operaciones. Ed. McGraw-Hill.
Hillier, F.S., Hillier, M.S. y Liebermann, G.J. (2000): Introduction to Management Science. A Modeling and Case Studies Approach with Spreadsheets. Irwin-McGraw-Hill.
Winston, W. (1994):Investigación de Operaciones. Aplicaciones y Algoritmos. Grupo Editorial Iberoamericano.
Winston, W. y Albright, S. C. (1997): Practical Management Science. Spreadsheet Modeling and Applications. Duxbury Press.
ENLACES
http://www.informs.org/
Página de INFORMS la Sociedad Americana de Investigación Operativa.
http://www.ifors.org/
Página de IFORS la Federación Internacional de Sociedades de Investigación Operativa.
http://opsresearch.com/cgi-bin/mainIndex.cgi/
Página de información genérica de Investigación Operativa.
http://www.orsoc.org.uk/
Página de OR Society la Sociedad Británica de Investigación Operativa.
Grupo de noticias /sci.op-research/ Es un grupo de noticias sobre temas de Investigación Operativa.
Proyecto e-Math - Financiado por la Secretaría de Estado de Educación y Universidades (MECD)
Técnica Administrativa, Buenos Aires, V. 5, nº 1, julio/septiembre 2005 - ISSN 1666-1680 -







2 Comments:
Felicidades, su blog esta muy bueno... espero que suba ejemplos de aplicacion a Bolivia.
Lo referenciare en mi blog http://investigacionoperativa.blogspot.com/
un saludo desde La Paz
me parece exelente su documento, pero busco tesis sobre busuqeda y detccion, no se si me pueda ayudar?
Post a Comment
<< Home